1.1 Кинематика

Механическое движение

Механическое движение — изменение положения тела относительно других тел с течением времени.

---

Для анализа и описания механического движения необходима система отсчета. Основные составляющие системы отсчета:

1. Тело отсчета (к примеру, Земля)
2. Система координат (чаще - ПДСК)
3. Часы, жестко связанные с системой отсчета

Материальная точка

Материальная точка — тело, размерами которого можно пренебречь в данной задаче. Основные случаи применимости модели материальной точки:

1. Пройденное телом расстояние много больше его характерных размеров
2. Тело движется поступательно (следующее положение любого отрезка на теле параллельно его предыдущему положению)

Путь, перемещение

Радиус-вектор $\vec{r}$ — вектор из начала координат в материальную точку. Радиус-вектор однозначно задает положение точки в пространстве. Его проекции:

$$\vec{r}=\left(\begin{array}{c}x(t)\\ y(t)\\ z(t)\end{array}\right)$$

Найти зависимости координат от времени - решить основную задачу механики.
Траектория — линия, вдоль которой движется тело.
Путь $S$ — длина траектории (то есть скаляр, а не вектор).
Перемещение $\vec{S}$ — вектор из начального положения тела в конечное. Связь с радиус-вектором:

$$\vec{S}=\overrightarrow{r_2}-\overrightarrow{r_1}$$

---

Введенные понятия наглядно показаны на рисунке:

---

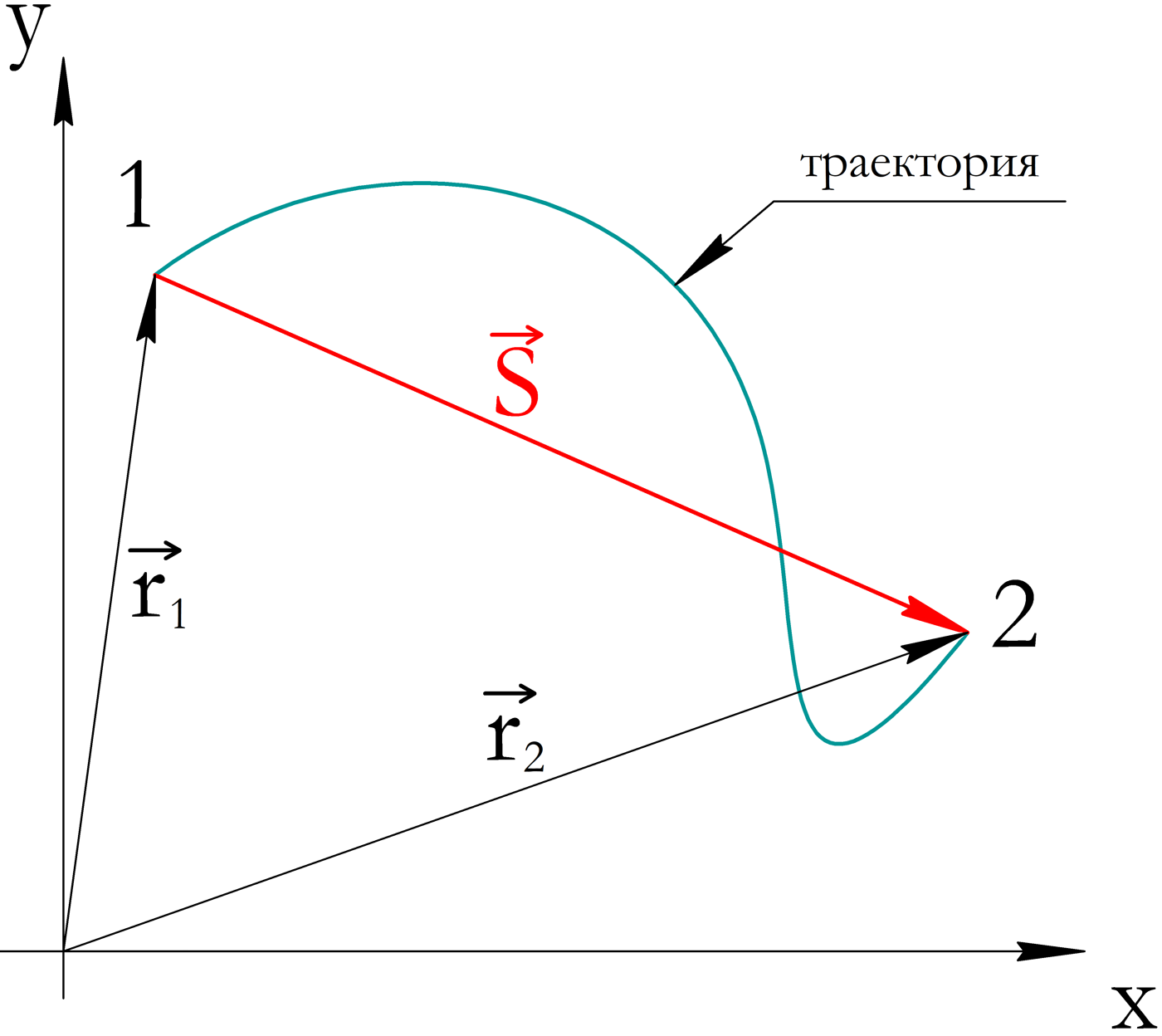
Для пути и перемещения всегда выполняется неравенство:

$$\boxed{|\vec{S}|\le S}$$

Скорость

Скорость материальной точки $\vec{v}$ — векторная физическая величина, характеризующая быстроту изменения положения.
Это определение не строгое и не полное, но вполне подходит для понимания того, что показывает скорость.
Мгновенная скорость — чисто математическое понятие, равное пределу отношения элементарного перемещения $\Delta \vec{S}$ к бесконечно малому промежутку $\Delta t$:

$$\vec{v}=\underset{\Delta t\to 0}{\lim }\frac{\Delta \vec{S}}{\Delta t}$$

Нас будет интересовать другая трактовка, более привычная человеку, знакомому с понятием производной. Согласно физическому смыслу производной, проекции вектора скорости равны производным от координат:

$$\boxed{v_x=x^{\prime }(t)}$$ $$v_y=y^{\prime }(t)$$

Ускорение

Ускорение материальной точки $\vec{a}$ — векторная физическая величина, характеризующая быстроту изменения скорости.
Строгое определение ускорения схоже с определением мгновенной скорости:

$$\vec{a}=\underset{\Delta t\to 0}{\lim }\frac{\Delta \vec{v}}{\Delta t}$$

Согласно физическому смыслу производной, проекция вектора ускорения равна первой производной скорости и второй производной координаты:

$$\boxed{a_x=v_x^{\prime }(t)=x^{\prime \prime }(t)}$$

Равномерное прямолинейное движение

Равномерное прямолинейное движение - движение с $\vec{v}=const$, т.е. скорость постоянна и по модулю, и по направлению. Возможен и другой случай: постоянство скорости лишь по модулю.
Постоянство скорости дает возможность перейти от предела при бесконечно малом времени $\Delta t\to 0$ к полному времени движения, отсчет которого начинается с 0:

$$v_x=\underset{\Delta t\to 0}{\lim }\frac{\Delta x}{\Delta t}=\frac{\Delta x}{\Delta t}=\frac{x(t)-x_0}{t}$$

Отсюда получим уравнение прямолинейного равномерного движения:

$$\boxed{x(t)=x_0+v_x\cdot t}$$

Важно! Уравнение $x(t)$ - линейная функция, поэтому его график - прямая.

---

На анимации ниже показано, как график координаты $x(t)$ (сверху) отражает действительное равномерное движение материальной точки по прямой (снизу).

---

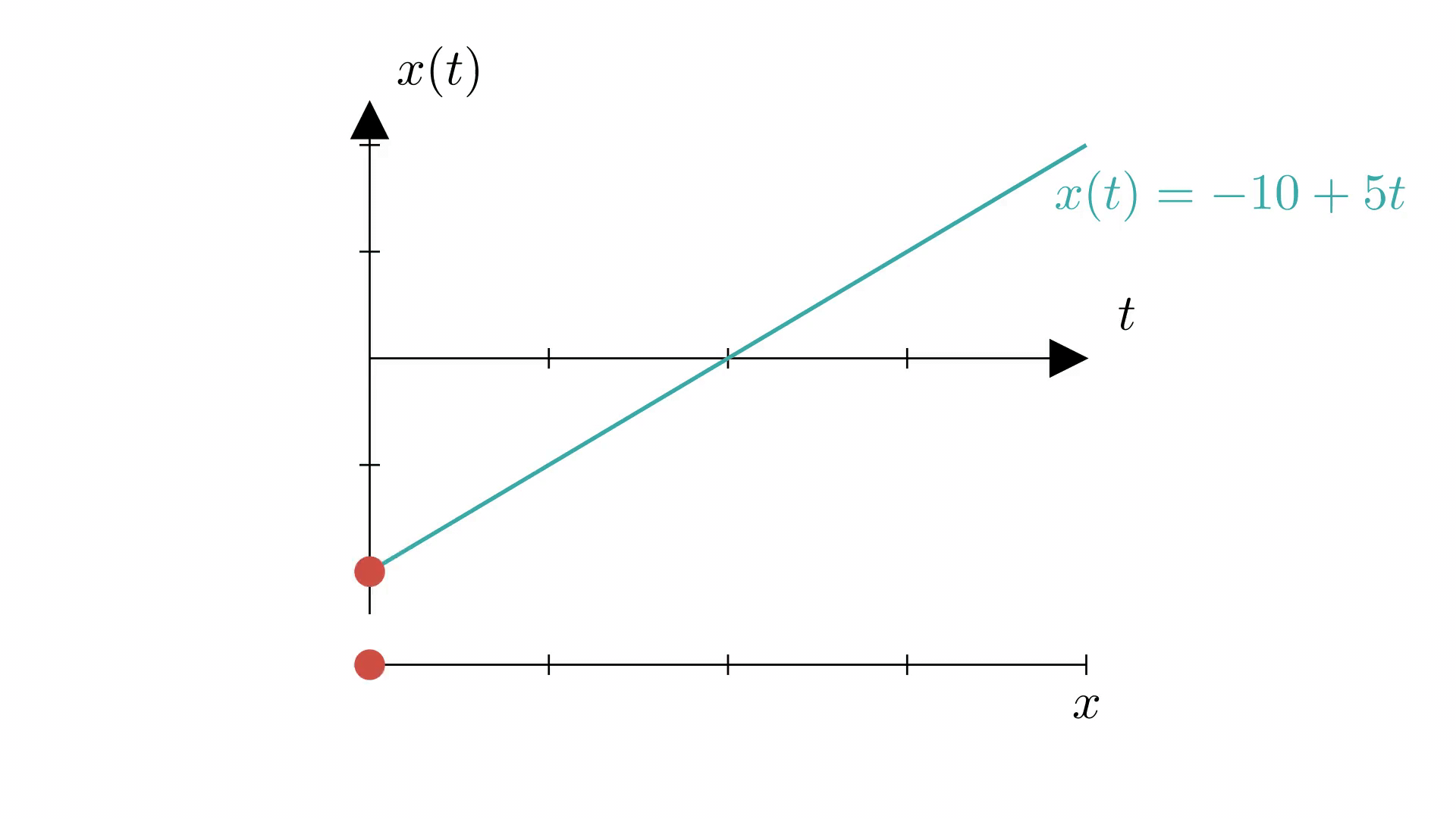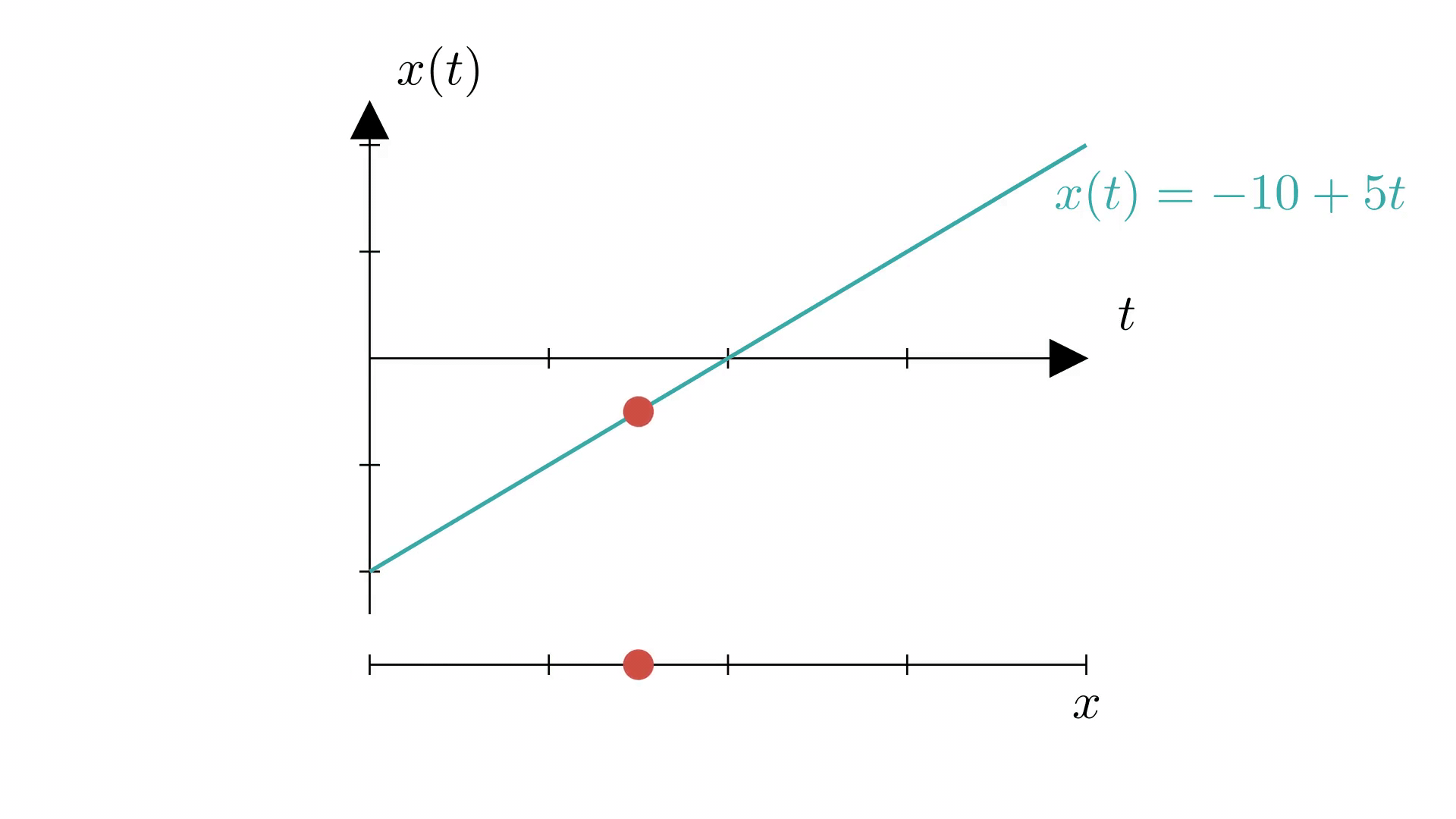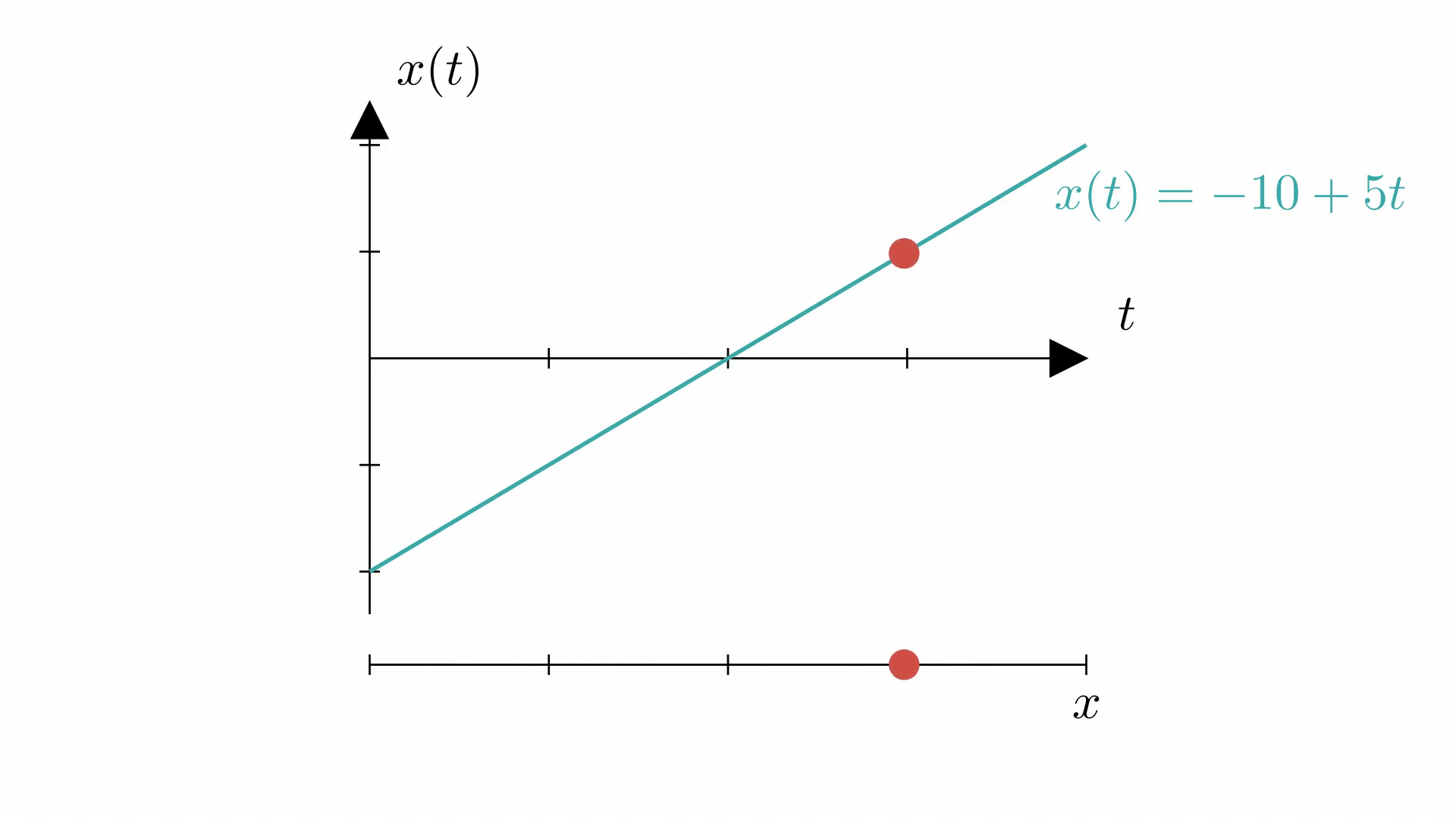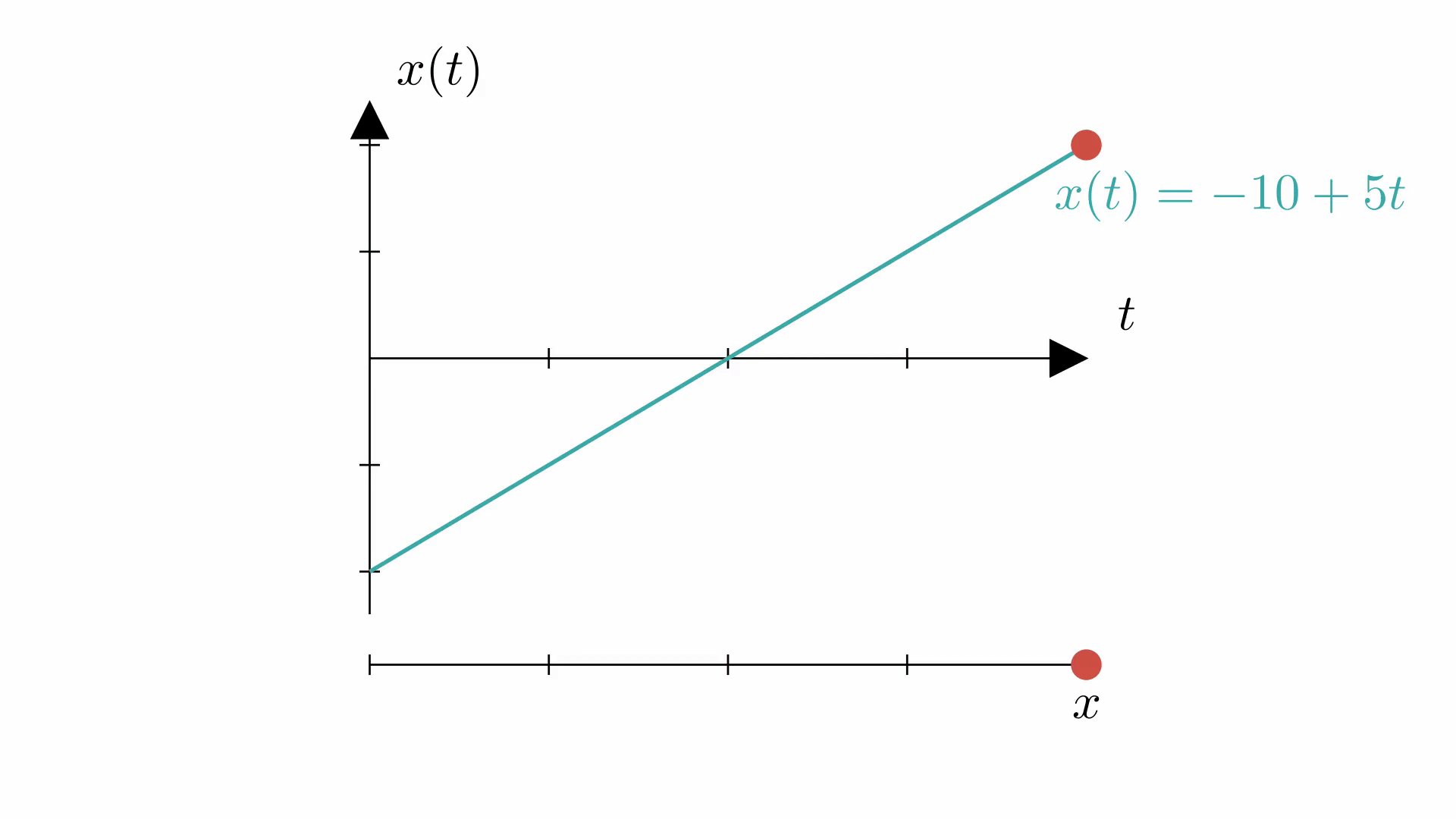
Равноускоренное прямолинейное движение

Равноускоренное движение — движение с $\vec{a}=const$, т.е. ускорение постоянно и по модулю, и по направлению.

Уравнение скорости

Из строгого математического определения ускорения можно вывести уравнение скорости при равноускоренном движении. Постоянство ускорения позволяет избавиться от предела и перейти к приращениям за конечный промежуток времени:

$$a_x=\underset{\Delta t\to 0}{\lim }\frac{\Delta v_x}{\Delta t}=\frac{\Delta v_x}{\Delta t}=\frac{v_x-v_{0x}}{t}$$

Отсюда получим уравнение проекции скорости $v_x$ при прямолинейном равноускоренном движении:

$$\boxed{v_x(t)=v_{0x}+a_x\cdot t}$$

где $v_{0x}$ — проекция начальной скорости на ось $x$;
$a_x$ — проекция ускорения на ось $x$;
$t$ — время движения.

Уравнение движения

Есть два способа получить уравнение движения.
Первый - честный - проинтегрировать уравнение скорости. Че за *** проинтегрировать? Нахождение интеграла уравнения скорости - все равно что нахождение функции, которая при взятии производной дает уравнение скорости:
Имеем уравнение скорости $v_x(t)=v_{0x}+a_x\cdot t$. Функция, которая при дифференцировании по переменной $t$ даст зависимость $v_x(t)$:

$$x(t)=x_0+v_{0x}\cdot t+\frac{a_x\cdot t^2}{2}$$

Те, кто знаком с понятием производной (Алгебра, 10 кл.), могут проверить: возьмите производную $x^{\prime }(t)$, учитывая, что $x_0,v_{0x},a_x$ — константы.
Второй - читерство чистой воды - посчитать площадь под графиком функции.

---

На рисунке ниже представлен произвольный график $v_x(t)$ в соответствии с уравнением скорости:

---

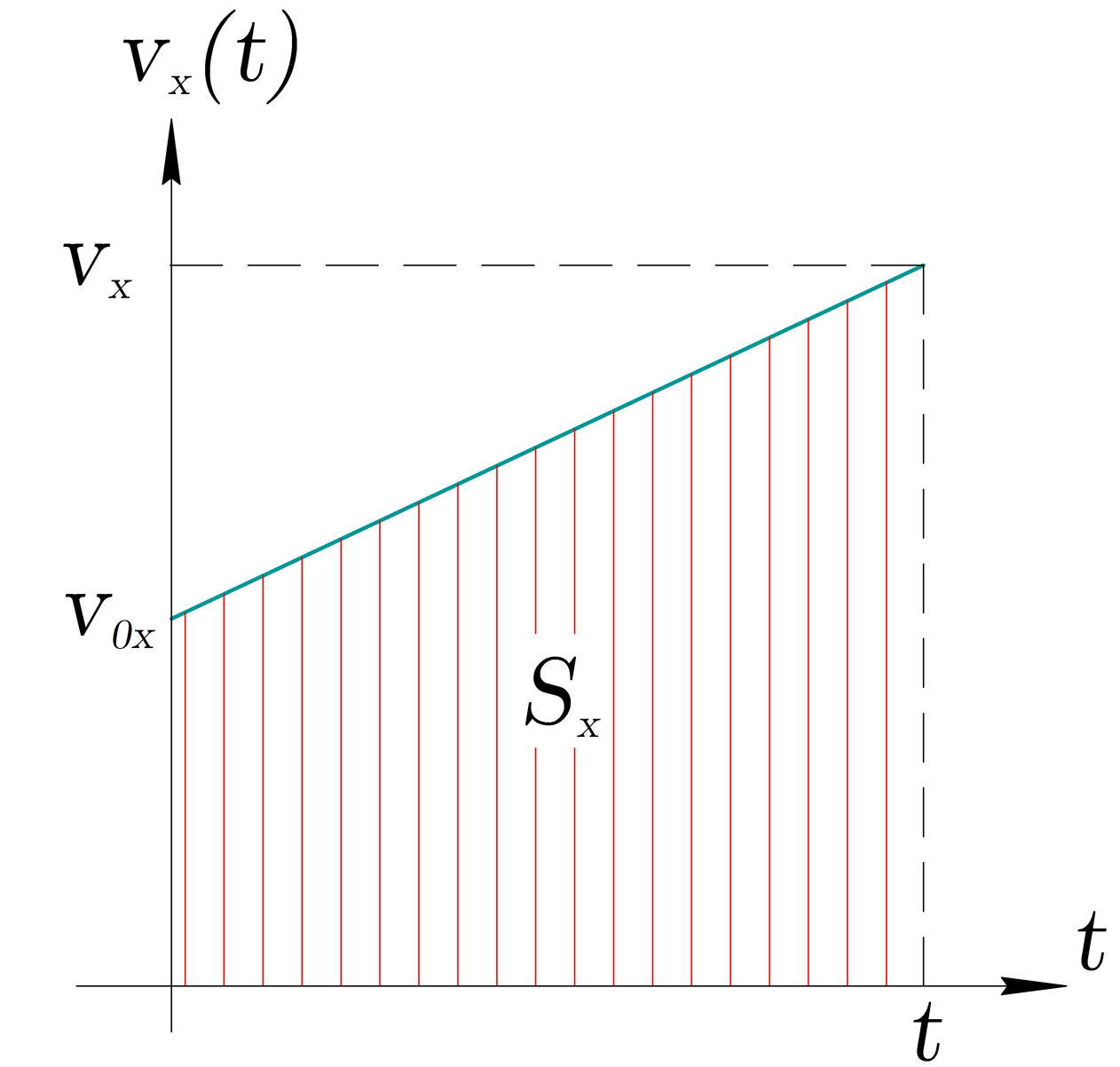
Площадь фигуры под графиком — площадь трапеции — равна проекции вектора перемещения:

$$S_x=\frac{v_x+v_{0x}}{2}\cdot t$$

Поставим вместо $v_x$ уравнение скорости:

$$S_x=\frac{v_{0x}+a_x\cdot t+v_{0x}}{2}\cdot t=v_{0x}\cdot t+\frac{a_x\cdot t^2}{2}$$

Так как $S_x=x(t)-x_0$ (смотри определение перемещения), то:

$$x(t)=x_0+S_x=x_0+v_{0x}\cdot t+\frac{a_x\cdot t^2}{2}$$

Любой из двух способов хорош и ведет нас к уравнению прямолинейного равноускоренного движения:

$$\boxed{x(t)=x_0+v_{0x}\cdot t+\frac{a_x\cdot t^2}{2}}$$

Выше показано, что проекция перемещения связана с $x(t)$:

$$\boxed{S_x=v_{0x}\cdot t+\frac{a_x\cdot t^2}{2}}$$

Из площади под графиком мы вывели формулу для проекции перемещения:

$$\boxed{S_x=\frac{v_x+v_{0x}}{2}\cdot t}$$

При подстановке в последнюю формулу времени, выраженного через уравнение скорости, получим:

$$S_x=\frac{v_x+v_{0x}}{2}\cdot t=\frac{v_x+v_{0x}}{2}\cdot \frac{v_x-v_{0x}}{a_x}=\boxed{\frac{v_x^2-v_{0x}^2}{2a_x}}$$

Важно! Ученик должен сам выбирать, какую из формул $S_x$ использовать, в зависимости от того, что «Дано» в задаче.

---

На анимации ниже показано, как график координаты $x(t)$ (справа) отражает действительное равноускоренное движение материальной точки по прямой (слева).

---

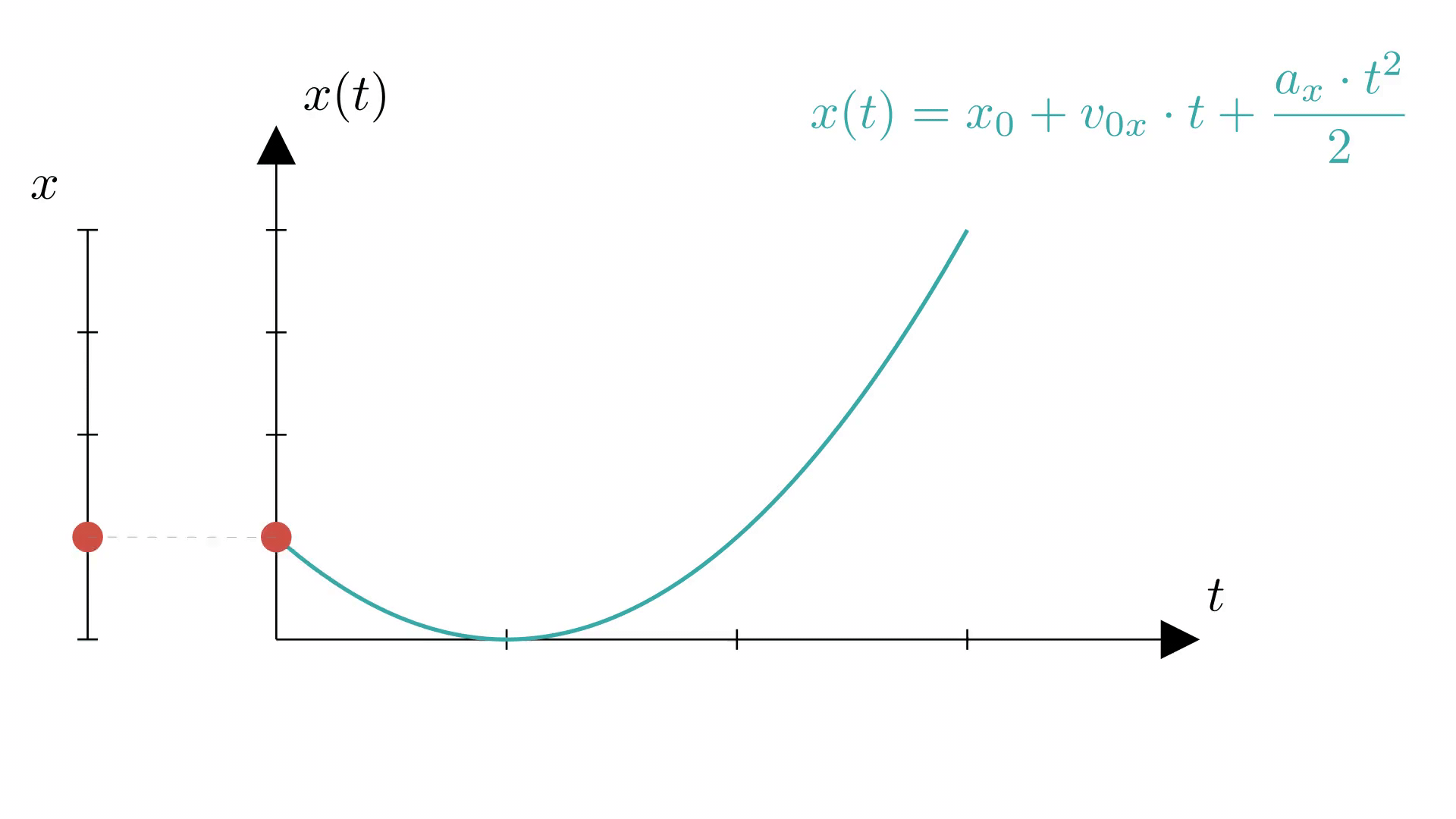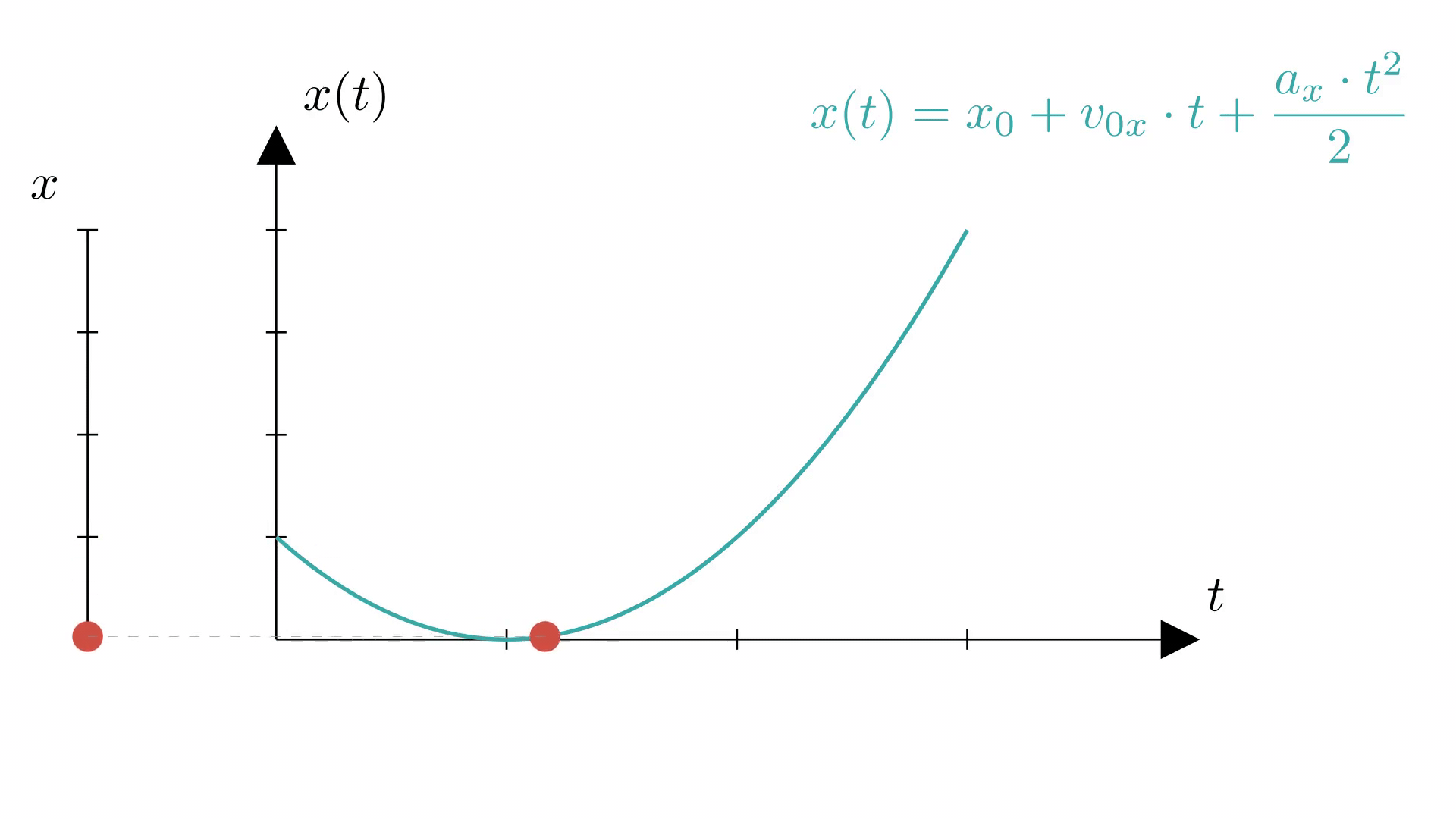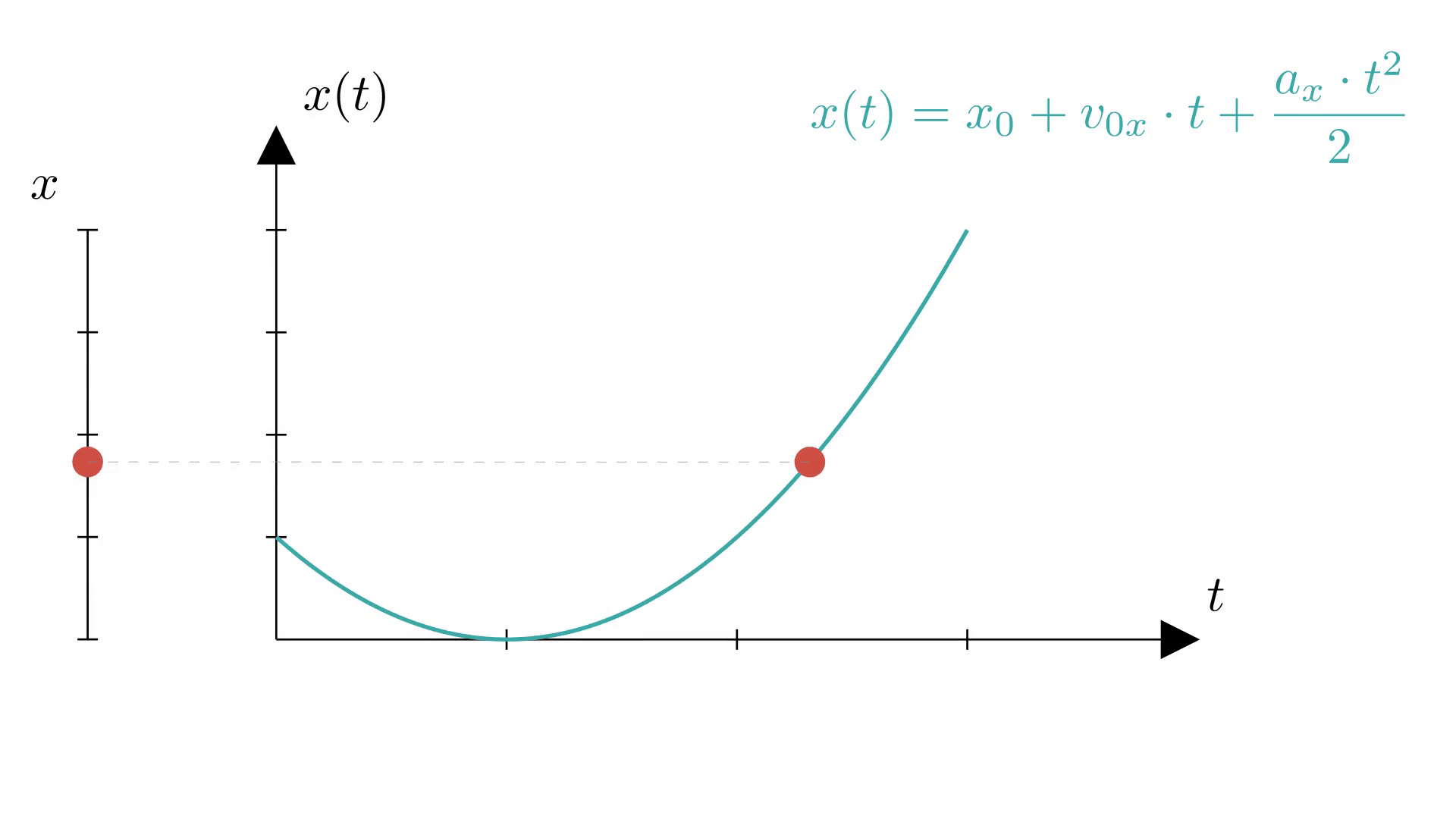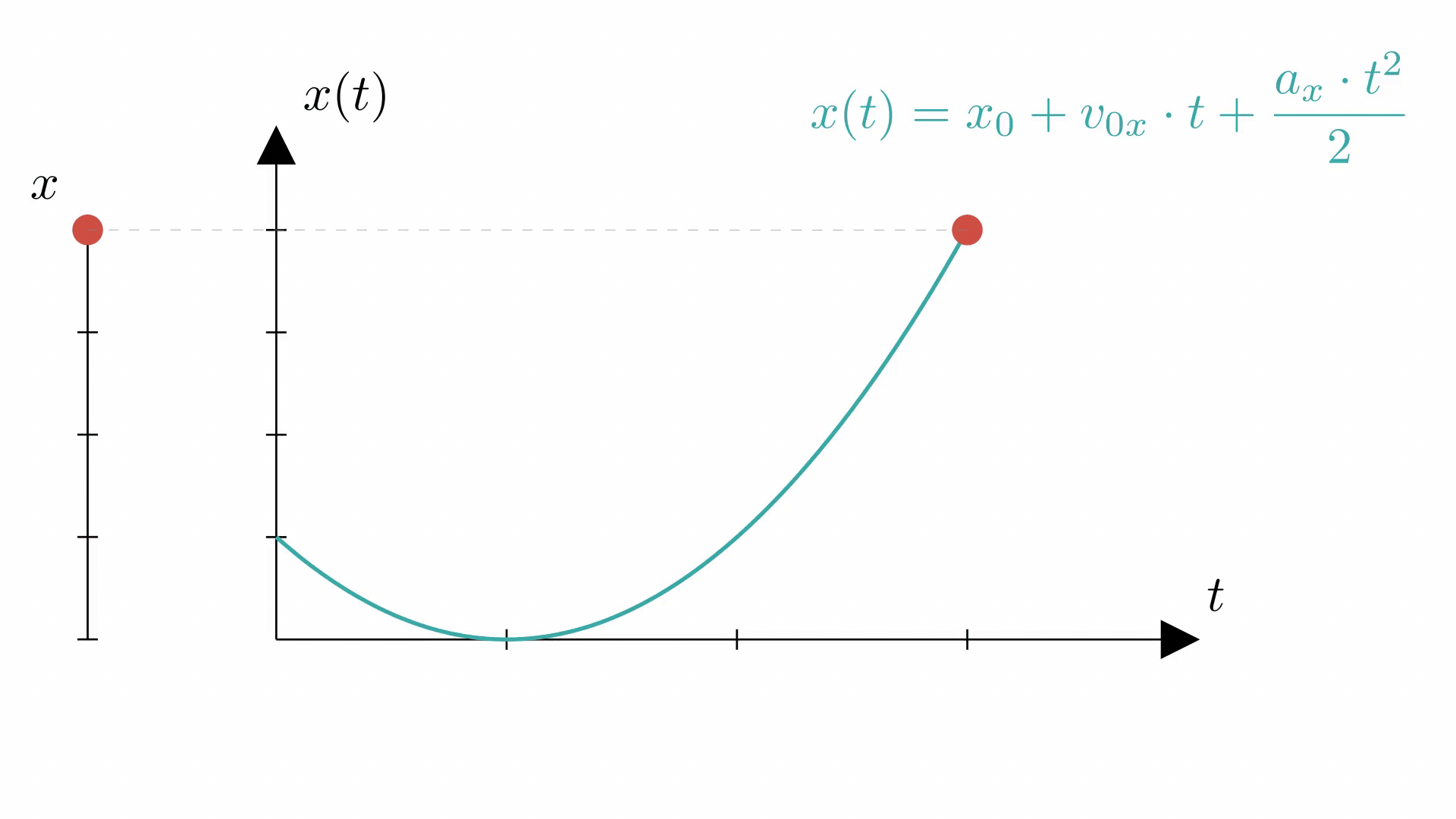
Баллистическое движение

Баллистическое движение — движение тела, брошенного под углом к горизонту, в поле силы тяжести.
Движение происходит под действием единственной силы ${\vec{F}}_{\text{тяж}}=m\cdot \vec{g}$, поэтому ускорение тела равно ускорению свободного падения $\vec{g}$.

---

На рисунке ниже показан классический пример броска тела под углом $\alpha$ к горизонту с начальной скоростью $\overrightarrow{v_0}$ и его дальнейшая траектория движения — парабола.

---

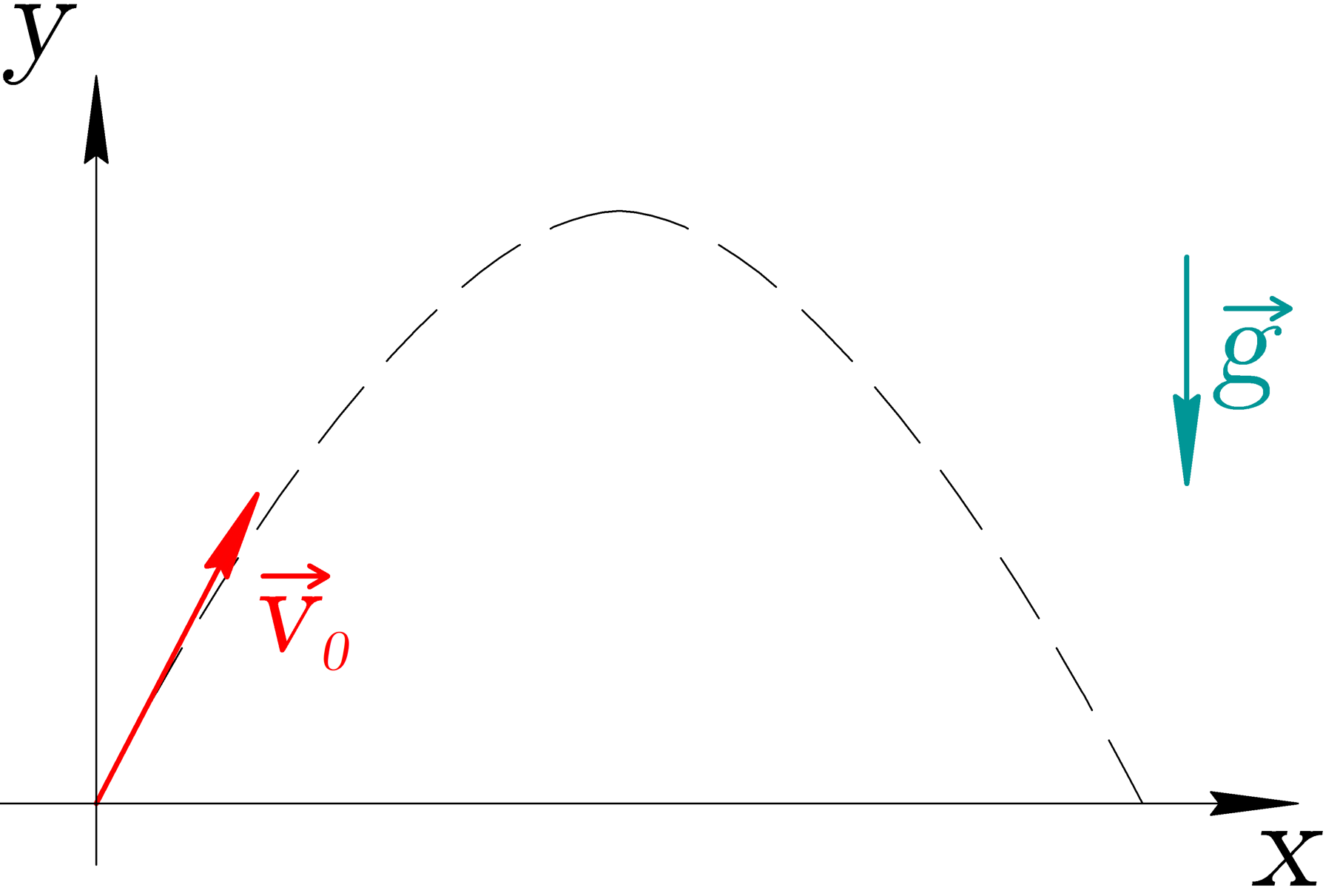
Проекции ускорения

Глядя на рисунок, определим проекции вектора ускорения на координатные оси:

$$\{\begin{array}{l}{a}_x=0\\ a_y=-g\end{array}$$

Проекции скорости

В правой части рисунка наглядно показано проецирование вектора начальной скорости $\overrightarrow{v_0}$. Зная проекции ускорения, определим уравнения скоростей при баллистическом движении:

$$\boxed{\{\begin{array}{l}{v}_x(t)=v_0\cos \alpha \\ v_y(t)=v_0\sin \alpha -g\cdot t\end{array}}$$

Важно! Посмотрите на характер изменения проекций скорости: движение по горизонтали происходит с постоянной скоростью, т.е. является равномерным, движение по вертикали происходит с постоянным ускорением, т.е. является равноускоренным.

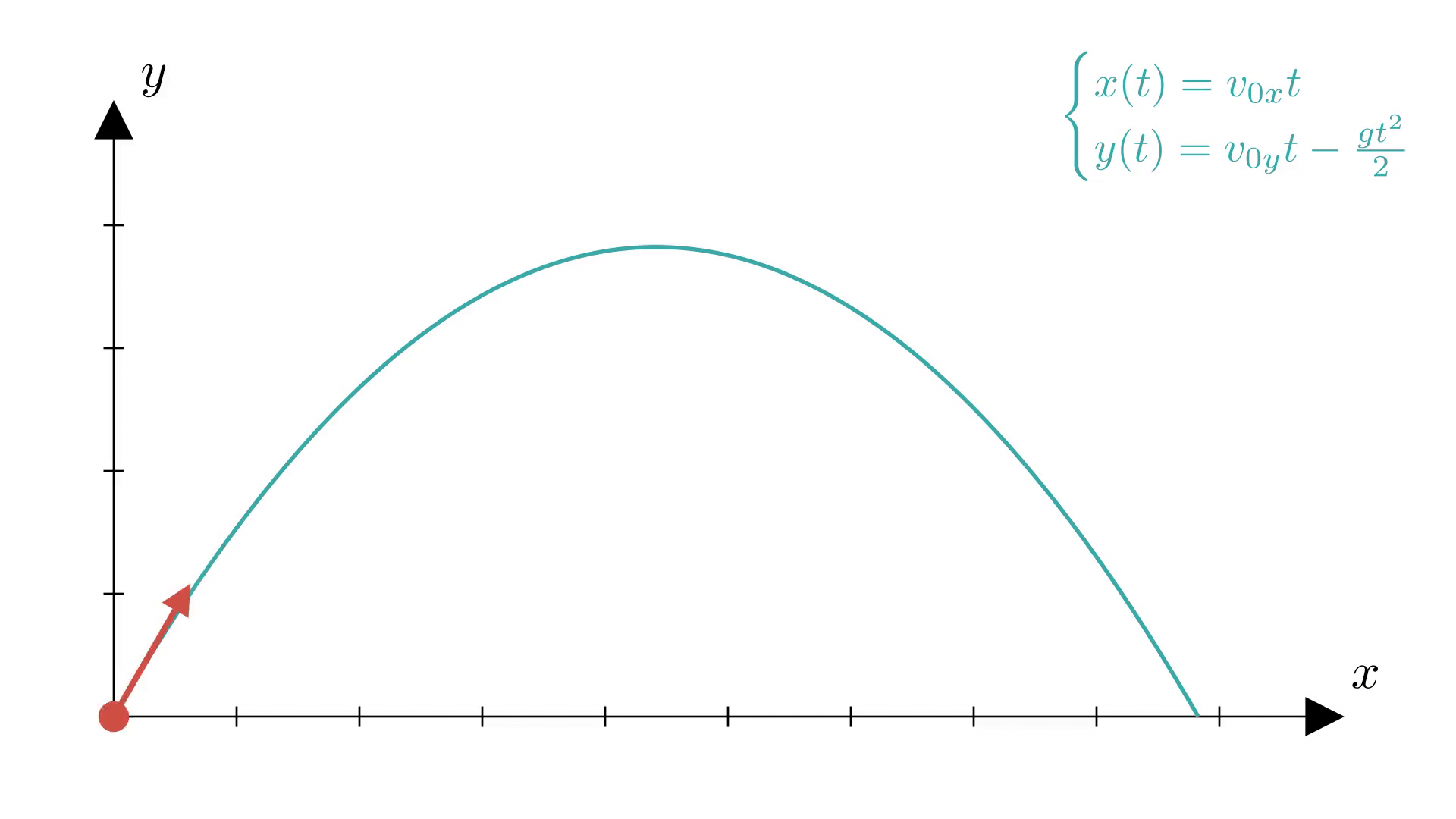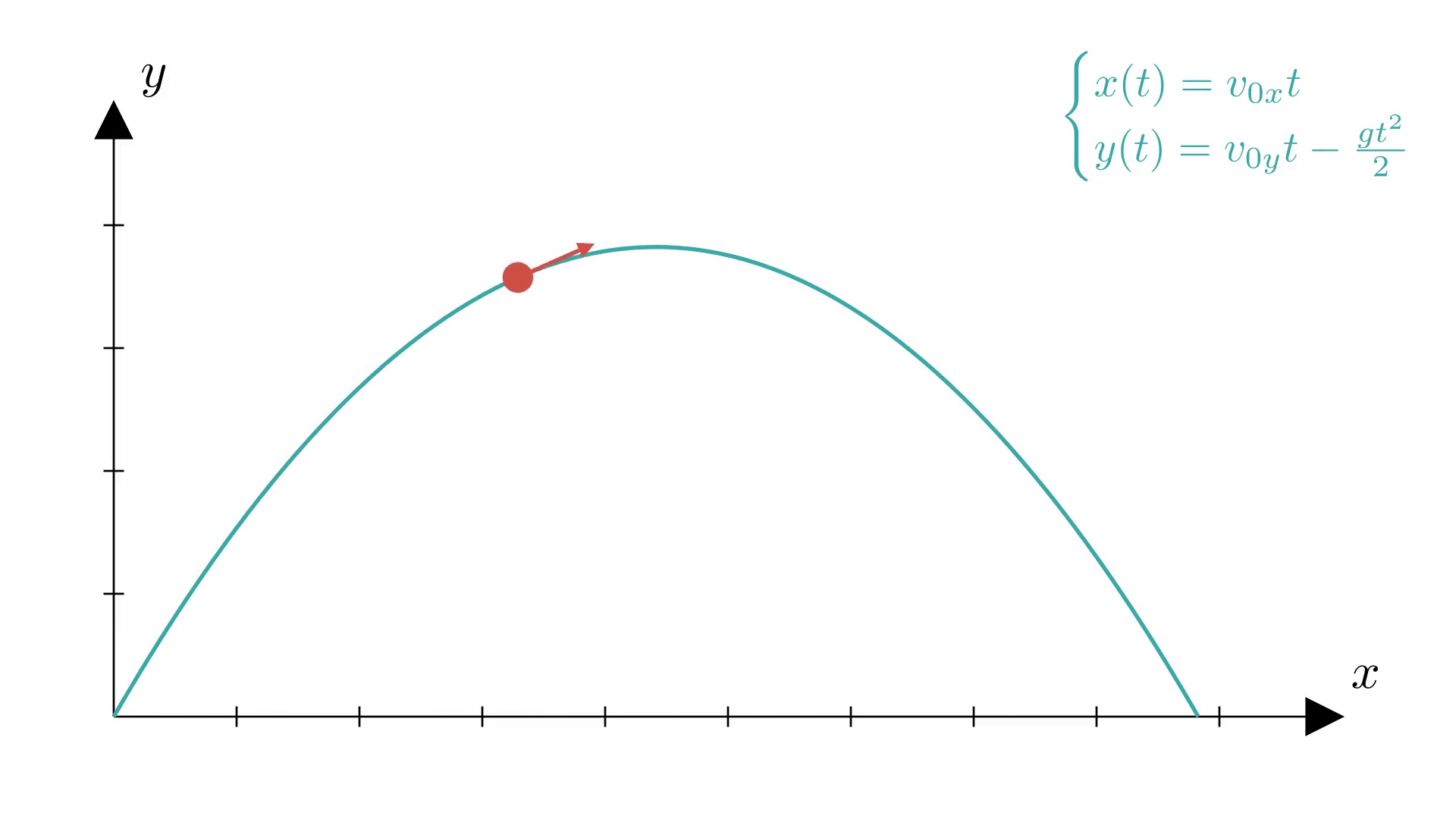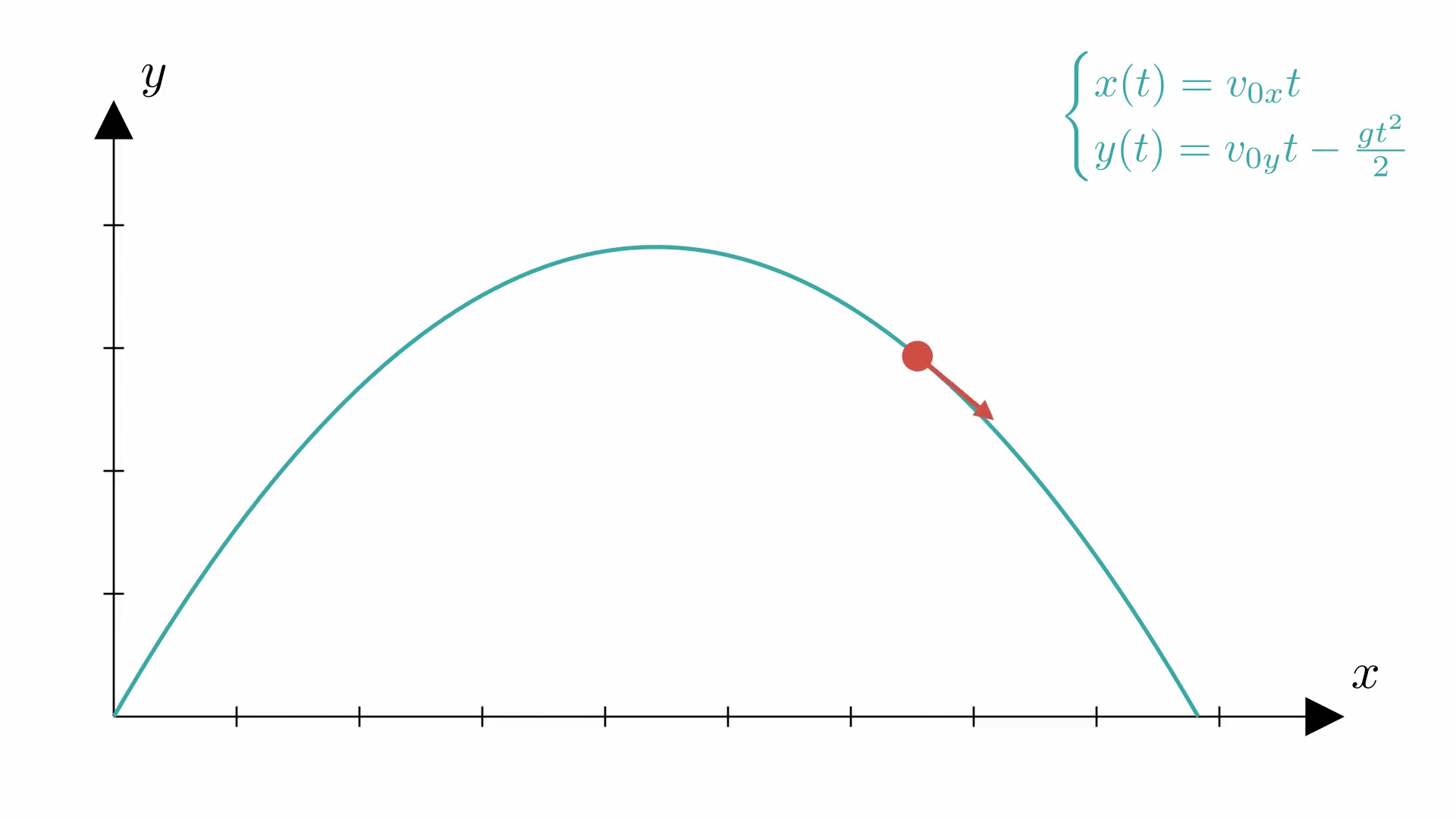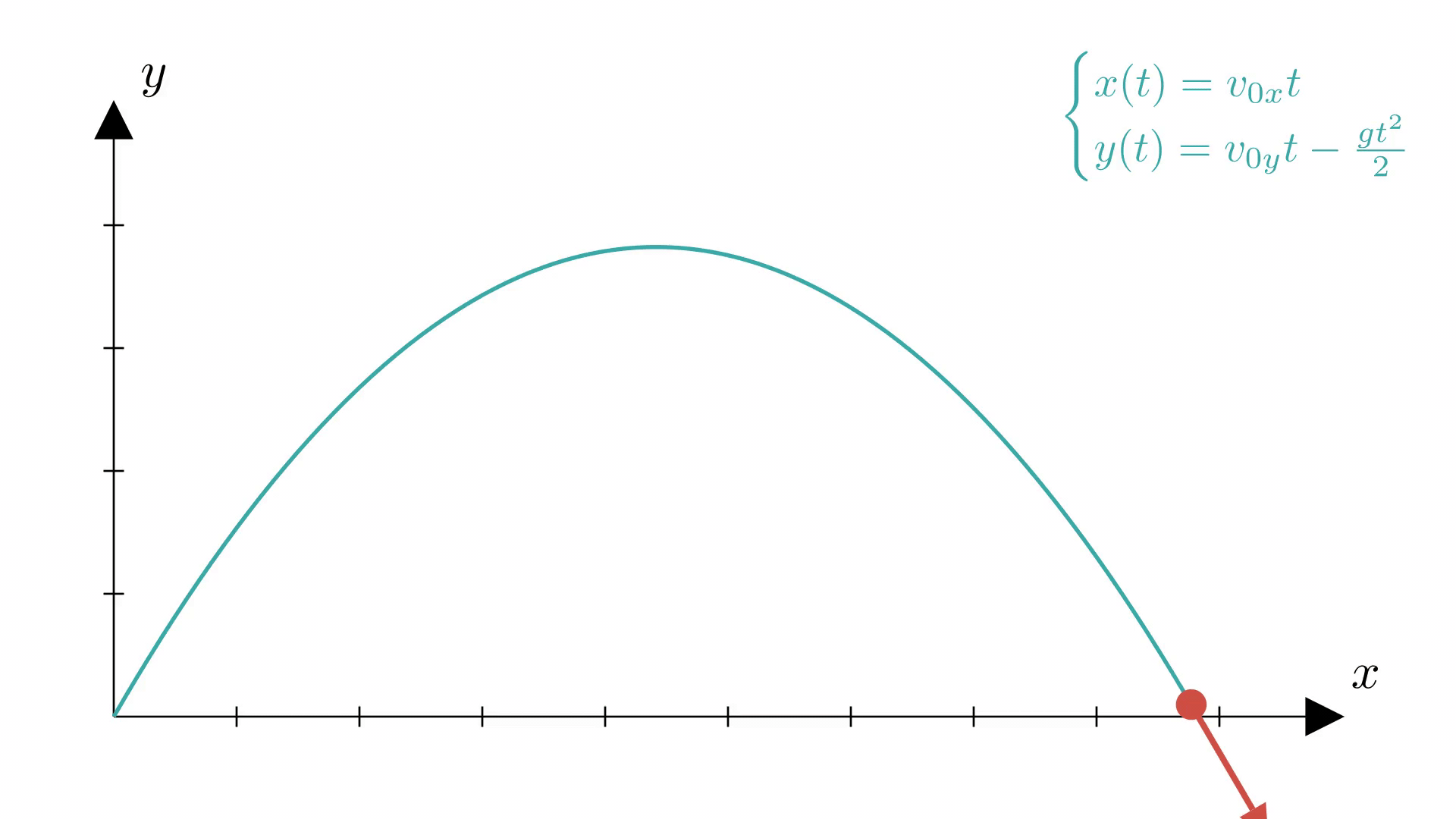
Уравнения баллистического движения

При броске с точки $\left(x_0;y_0\right)$ с начальной скоростью $\overrightarrow{v_0}$ уравнения координат при баллистическом движении будут выглядеть следующим образом:

$$\boxed{\{\begin{array}{l}x(t)=x_0+v_0\cos \alpha \cdot t\\ y(t)=y_0+v_0\sin \alpha \cdot t-\frac{g\cdot t^2}{2}\end{array}}$$

Заметим, что уравнение $x(t)$ соответствует уравнению равномерного движения, а уравнение $y(t)$ — уравнению равноускоренного движения.

Время подъема, время полета

Время подъема — время движения до наивысшей точки траектории, т.е., в случае баллистического движения, до вершины параболы.
Время подъема можно найти из того условия, что в вершине обнуляется вертикальная проекция скорости $v_y$, так как тело разворачивается в своем движении по вертикали. Имеем:

$$v_y(t)=v_0\sin \alpha -g\cdot t=0\Rightarrow \boxed{t_{\text{подъема}}=\frac{v_0\sin \alpha }{g}}$$

Время подъема — время, за которое координата $y(t)$ обратится в ноль. При броске с нулевой вертикальной координаты (с уровня земли) можно воспользоваться «симметрией» параболы:

$$\boxed{t_{\text{полета}}=2\cdot t_{\text{подъема}}=\frac{2\cdot v_0\sin \alpha }{g}}$$

---

На анимации ниже показано, как меняется направление вектора скорости $\vec{v}$ по мере подъема тела при баллистическом движении. Обратите внимание на то, что вектор скорости горизонтален в наивысшей точке траектории, т.е. в вершине $v_y=0$.
Заметим, что по мере подъема модуль (длина) вектора скорости уменьшается от $v_0$ в точке старта до $v_0\cdot \cos \alpha$ в вершине параболы.

---

Равномерное движение по окружности

Равномерное движение по окружности — движение с $\boxed{|\vec{v}|=const}$, при этом траекторией материальной точки является окружность.